Understanding AC Circuits-Help Wanted

[James Collins]

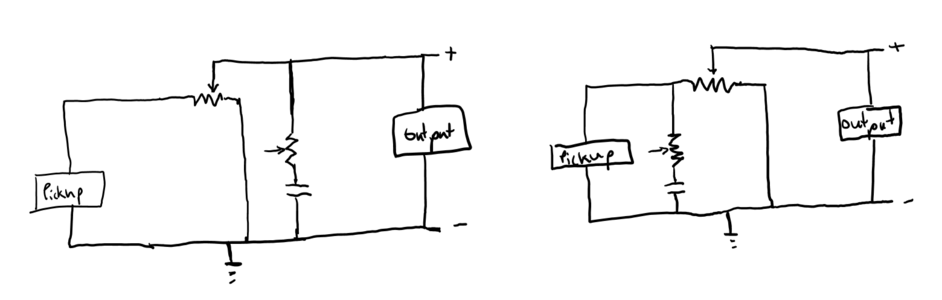
I'm trying to dive deep on my understanding of guitar circuits than my current superficial one.

First question: Is it pretty useless to try to create equations for simple circuits like you would for direct current and resistor circuits? I tried doing it for these two circuits (Single pickup/Volume/Tone) and ended up with some relatively monstrous equations for what I think are really simple circuits.

Forgive me if those are incorrectly drawn, but my equations I came up with for these were:
if the volume pot has a total resistance "x",
and resistance between lug 3 and 2 is "a" on the volume pot,
and resistance across the tone pot to the capacitor is "b",
and capacitance is "C", then

The circuit on the left has total impedance;
Z1 = (xa +xb+xC-a^2)/(x-a+b+C)

The circuit on the right has total impedance;
Z2 = (xb+xC)/(x+b+C)

Also, if you had a bypass switch for the tone, the total impedance be
Zbypass = x = the total resistance of the volume pot when the switch is open
I did think this last one was interesting because it means total impedance depends on the size of the potentiometer and not on the position of the potentiometer.
===========================================
Second question: Am I correct with the following: Total impedance in a circuit is going to be different at different frequencies due to capacitance and inductance being relative to frequency? Increased capacitive reactance will result in more impedance for higher frequencies. Increased inductive reactance will result in more impedance for lower frequencies. Adding a capacitor into the circuit will produce more impedance of lower frequencies. Depending on the circuit therefore either higher or lower frequencies will be impacted more by the impedance.

Third question: I have read on guitar electronic sites, that high frequency signals have an easier time crossing resistors. However, on physics websites, resistors have static values independent of the frequency of the current and should reduce the current for a given voltage the same regardless of the frequency. I'm inclined to believe the physics sites. For a simple circuit with a single volume pot like this:

It is commonly believed that low resistance pots (250k) are darker sounding than higher resistance pots (500k+). I understand that even with the volume all the way up, there is a connection across the resistor to ground that will reduce the overall current. Even if the output was very low impedance, the resistor would slightly reduce the current because total impedance would be slightly decreased.

But why does that affect high frequencies more?

Is the darkening of sound with lower resistors actually caused by decreased total resistance/impedance in the circuit which increases the amplitude of all frequencies of current and the fact that a lower pitched sound transfers through media (air/water/houses) more easily, so the perceived volume increase seems greater for lower pitched sounds? I think about it like the string section in an orchestra. Increasing the volume equally is like having the same number of violins, violas, cellos, and contrabasses. To have equal perceived volume it is actually violins > violas > cellos > contrabasses.

Fourth question: Do any guitar or bass circuits use inductors? An inductor would work like a capacitor allowing low frequencies to pass. A bass tone pot seems like it could be made with an inductor.

Thanks in advance to anyone that helps out. My head just exploded.

 

[Passinwind]

Fourth question: Do any guitar or bass circuits use inductors?

Yes, inductance is a vital component of a magnetic pickup's impedance. There's a smaller capacitive component as well. So all your models need to account for R,L and C vectors in the pickup.

Beyond that, look at Varitone circuits for one possible way of using one or more inductors.

 

[megafiddle]

First question: Is it pretty useless to try to create equations for simple circuits like you would for direct current and resistor circuits?

Not useless, but far from simple.

The basic forms for series and parallel impedance are no different than the forms for series and parallel resistance. For example, total Z for a series impedance is Z1 + Z2. Total Z for parallel impedance is (Z1 x Z2) / (Z1 + Z2).

The problem is that Z is a complex value and cannot be simply added, multiplied, or divided. It has a real resistive component and an imaginary reactive component.

From my own notes:

That can be somewhat simplified if combining just a capacitive reactance with a resistance in parallel, for example, but once combined, the full complex form of the combination needs to be used for subsequent calculations.

Also, the pickup itself consists of an inductance in series with a resistance, and that series combination is in parallel with the coil capacitance.

The equations above are for the special case of just two impedances in parallel. For more than two, the general form of reciprocal of sum of the reciprocals could be used, but then it can become really monstrous. Simpler to just combine two parallel branches at a time.

Series impedances are much simpler:

And of course the results are only true for a specific frequency.

-

 

[James Collins]

Not useless, but far from simple.

The basic forms for series and parallel impedance are no different than the forms for series and parallel resistance. For example, total Z for a series impedance is Z1 + Z2. Total Z for parallel impedance is (Z1 x Z2) / (Z1 + Z2).

The problem is that Z is a complex value and cannot be simply added, multiplied, or divided. It has a real resistive component and an imaginary reactive component.

From my own notes:

View attachment 3383123

That can be somewhat simplified if combining just a capacitive reactance with a resistance in parallel, for example, but once combined, the full complex form of the combination needs to be used for subsequent calculations.

Also, the pickup itself consists of an inductance in series with a resistance, and that series combination is in parallel with the coil capacitance.

The equations above are for the special case of just two impedances in parallel. For more than two, the general form of reciprocal of sum of the reciprocals could be used, but then it can become really monstrous. Simpler to just combine two parallel branches at a time.

Series impedances are much simpler:

View attachment 3383206

And of course the results are only true for a specific frequency.

-

As part of the reason then that a higher resistance potentiometer causes a brighter sound is that the additional resistance adds to the impedance of the pickup? I was reading some about peak frequency shifting, but all of the explanations I have read seem incomplete.

I think the other part that becomes confusing to me when writing equations is the ranges of resistances in addition to the ranges of frequencies.

 

[megafiddle]

Second question: Am I correct with the following: Total impedance in a circuit is going to be different at different frequencies due to capacitance and inductance being relative to frequency?Increased capacitive reactance will result in more impedance for higher frequencies. Increased inductive reactance will result in more impedance for lower frequencies. Adding a capacitor into the circuit will produce more impedance of lower frequencies. Depending on the circuit therefore either higher or lower frequencies will be impacted more by the impedance.

Partially correct. Increased reactance, either inductive or reactive, will result in increased impedance.

At audio frequencies, inductance and capacitance are more or less constant and mainly based on the physical properties of the components. It is the reactance that varies with frequency. Inductive reactance increases with frequency. Capacitive reactance decreases with frequency.

The effect that a capacitor or inductor has on the signal depends on it's location in the signal path. The typical tone circuit is in parallel with the pickup signal, between signal and ground. As the frequency increases, the capacitive reactance decreases, losing more of the higher frequencies. If that same cap were in series with the signal, it would pass more high frequencies through as the reactance decreased.

An inductor would have the opposite effect, but with a different rolloff curve. If you were to replace the tone cap with a "tone coil", the reactance would decrease with frequency, and lose more of the lower frequencies. The rolloff would be different because the signal source impedance is itself partly inductive. It's never simple.

-

 

[megafiddle]

As part of the reason then that a higher resistance potentiometer causes a brighter sound is that the additional resistance adds to the impedance of the pickup? I was reading some about peak frequency shifting, but all of the explanations I have read seem incomplete.

It does increase the total impedance of the circuit, but the difference is mainly due to the pickup signal itself having a large source impedance that increases with frequency. The signal originates in the pickup, but must pass through the pickup coil resistance and reactance. So the signal becomes divided between this internal pickup impedance, and the external potentiometer resistance. Since the pickup is inductive, this forms an LR lowpass filter. As the signal increases in frequency, more of the signal is lost across the internal impedance of the pickup, and less appears across the pot. If you reduce the pot resistance, even more of these high frequencies are lost across the pot and these losses also begin occurring at a lower frequency.

I think the other part that becomes confusing to me when writing equations is the ranges of resistances in addition to the ranges of frequencies.

Are you referring to things like kilohm, megohm, kHz?

-

 

[megafiddle]

Third question: I have read on guitar electronic sites, that high frequency signals have an easier time crossing resistors. However, on physics websites, resistors have static values independent of the frequency of the current and should reduce the current for a given voltage the same regardless of the frequency. I'm inclined to believe the physics sites.

At bass instrument frequencies, resistors are resistors. Their resistive value is independent of frequency. The StewMac article is an oversimplification of how pot resistance affects tone. Go with the physics sites.

You will often hear that the tone cap "dumps" or "bleeds off" highs to ground. This is also a oversimplification. The explanation works fine for it's intended purpose, but it's technically incorrect. Place that same tone cap on the amp output, and you lose virtually no highs at all. More on this below.

It is commonly believed that low resistance pots (250k) are darker sounding than higher resistance pots (500k+). I understand that even with the volume all the way up, there is a connection across the resistor to ground that will reduce the overall current. Even if the output was very low impedance, the resistor would slightly reduce the current because total impedance would be slightly decreased.

But why does that affect high frequencies more?

This is only partly due to the pot resistance. The other factor is the signal source impedance.

You basically have a signal divider, with the source signal divided between the source impedance and the pot, which are in series. The output signal appears at the junction of the source impedance and the pot. So a portion of the source signal will appear across the source impedance, and a portion of the signal will appear across the pot resistance. The proportions will depend on the relative impedances of these two elements. The portion across the pot is the output signal.

The relative proportions depend on the relative impedances of these two elements. At low frequencies, the source impedance is low, as it is partly inductive. So only a small portion of the signal is lost across the source impedance, and a large portion remains across the pot as output. As the frequency increases, more and more signal is lost across the source impedance and less remains across the pot as output.

If you changed the pot value, it would have little effect on the low frequencies since the pot resistance would still be relatively high compared to the source impedance.
But at higher frequencies, where the source impedance is much higher, the change in pot resistance is more significant.

You might think of the pot as having a loading effect on the pickup. A lower resistance pot loads down the pickup more, reducing the signal. But the loading effect also depends on frequency. Because the pickup has a higher source impedance at higher frequencies, it is also more easily loaded down at higher frequencies. So the presence of the pot resistance is going to produce a high frequency rolloff, and a lower resistance pot will start rolling off at a lower frequency.

Is the darkening of sound with lower resistors actually caused by decreased total resistance/impedance in the circuit which increases the amplitude of all frequencies of current and the fact that a lower pitched sound transfers through media (air/water/houses) more easily, so the perceived volume increase seems greater for lower pitched sounds? I think about it like the string section in an orchestra. Increasing the volume equally is like having the same number of violins, violas, cellos, and contrabasses. To have equal perceived volume it is actually violins > violas > cellos > contrabasses.

There are nonlinearities in our hearing that affect perceived frequency response based on loudness, but the effects of the bass tone circuitry are due to actual changes in the circuit's frequency response. In other words, after normalizing the volume, the frequency response change is still there.

-